Themen / Angebote für Arbeiten

Diese Arbeit wird zusammen mit dem Deutschen Zentrum für Luft- und Raumfahrt (DLR), Institut für Flugzeugführung, Braunschweig durchgeführt.

Hintergrund: Ein Verlust des Situationsbewusstseins ist der maßgebliche Auslöser für militärische Flugunfällen von Hubschraubern während der Landung. Durch das Aufwirbeln von Staub, auch Brown-out genannt, wird den Piloten kurz vor der Landung die Sicht genommen. Forschung und Wissenschaft beschäftigt sich mit Technologien zur Aufrechterhaltung des Situationsbewusstseins in solchen Situationen. Durch Verwendung von Sensoren sollen Messdaten über die Beschaffenheit der Landezone vor und während des Brown-outs gewonnen werden. Mit Hilfe dieser Daten wird den Piloten ein Geländemodell angezeigt, dass es erlaubt auch ohne tatsächliche Referenzen in der Außensicht sicher zu landen. Verschiedene Sensoren mit unterschiedlichen Meßmethoden kommen dabei zum Einsatz. Ein vielversprechender Sensor ist das AI-130 Millimeterwellen Radar.

Im Rahmen des DLR Projekts ALLFlight wird dieser Sensor am Forschungshubschrauber FHS (EC135) getestet. Die gewonnenen Daten sollen in einer Echtzeitanwendung auf einem Anzeigesystem im Hubschrauber dargestellt werden. Um die Daten in dieses Display integrieren zu können, soll eine Kartendarstellung entwickelt werden, die es erlaubt mit unterschiedlichen Daten verschiedener Quellen und variierender Auflösung arbeiten zu können. Gerade die variierende Auflösung der gesammelten Daten erschwert die Fusion von Daten über der Zeit.

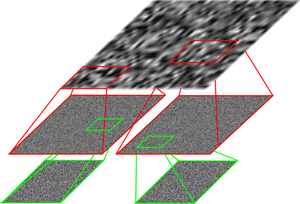
Aufgabe: Die Aufgabe besteht in der Entwicklung einer Datenstruktur zur Darstellung eines Oberflächenmodells für die Pilotenanzeige. Besonderes Augenmerk soll auf die Fusion von Messdaten des Geländes liegen und dabei sowohl die unterschiedliche Auflösung als auch die zeitliche Differenz der gesammelten Daten berücksichtigt werden. In Abhängigkeit zur Gefährdung des Hubschraubers (z.B. Entfernung zum Hubschrauber und zur geplanten Route) soll das qualitativ beste und möglichst geschlossene Oberflächenmodell bestimmbar sein. Ein möglicher Lösungsweg ist die Verwendung von „Level-Of-Detail“ Datenstrukturen. Dabei werden neue Daten in eine Hierarchie von unterschiedlichen Auflösungsstufen jeweils nur in der passenden „Schicht“ eingefügt, um später transparent in allen Sichten präsent zu sein. Ziel ist es, die Daten effizient und verlustfrei zu speichern.

Vorkenntnisse: Der Kandidat sollte Kenntnisse in elementarer Geometrie, Vektorrechnung und Programmierung haben. Mindestanforderung ist die Beherrschung von C, Java oder C++. Desweiteren sind grundlegende Kenntnisse der Computergrafik förderlich.

Ein wichtiges Hilfsmittel in der Modellierung von Freiformflächen ist das Aufschneiden von Flächen entlang vorgegebener Kurven (sog. trimming). Dies findet zahlreiche Anwendungen, beispielsweise im Karosserie-Design. Eine Möglichkeit solche Flächenkurven zu beschreiben ist die orthogonale Projektion einer Raumkurve auf die Fläche um eine Flächenkurve zu erhalten. Dabei wird die Flächenkurve mit der Raumkurve durch Geraden verbunden, die entlang der Flächennormalen verlaufen.

Ziel dieser Arbeit ist die Untersuchung und Implementierung von robusten numerischen Verfahren zur Berechnung dieser Projektion. Einige existierende Verfahren [1,2] basieren auf der Integration eines Systems gewöhnlicher Differentialgleichungen im Parameterraum der Fläche, wodurch die Flächenkurve ausgehend von einem Startpunkt stückweise trassiert wird. Ein ähnlicher Ansatz kann auch im Falle implizit definierter Flächen verfolgt werden. In beiden Fällen können Singularitäten auftreten, die numerische Schwierigkeiten bereiten und zu einem Abbruch der Trassierung führen. Im Rahmen dieser Arbeit sollen die auftretenden Schwiergkeiten genauer untersucht und Lösungsvorschläge erarbeitet werden.

Erforderlich sind Programmierkenntnisse (vorzugsweise C++). Hilfreich sind Kenntnisse in den Bereichen Computergrafik und Berechnende Geometrie. Für die Implementierung wird ein bereits existierendes Framework zur Verfügung gestellt.

[1] Pegna, J.; Wolter, F.-E., "Surface curve design by orthogonal projection of space curves onto free-form surfaces", (1996), 45-52, J. MECH DESIGN 118 (1): 45-52 MAR 1996 ftp://ftp.gdv.uni-hannover.de/papers/wolter1996-surf_curve.pdf

[2] Pegna, J.; Wolter, F.-E., "Designing and Mapping Trimming Curves on Surfaces Using Orthogonal Projection", Proceedings of the 15th ASME Design Automation Conference: Advances in Design Automation, (B. Ravani, ed.), vol. 1, NY: ASME, 1990, p. 235-245,  ftp://ftp.gdv.uni-hannover.de/papers/wolter1990-trimming_curves.pdf

Durch das Aufkommen von billigen 3D-Scannern und immer besserer Modelliersoftware steigt die Anzahl von 3D-Modellen im Internet rasant. Diese Modelle sind meist durch Eckpunkten und Dreiecke gegeben. Um ein einzelnes Modell in dieser Form in einer großen Datenbank zu finden, ist es bisher notwendig, diese Modelle mit guten Meta-Informationen zu versehen. Neue Methoden versuchen, diese Problematik zu umgehen, indem sie die Meshes mit verschiedenen Verfahren direkt vergleichen. Ziel dieser Arbeit ist es, eine Anwendung zu entwickeln, die 3D-Modelle mit dem so genannten "Shape-DNA"-Verfahren vergleicht. Diese soll eine GUI und eine Datenbank für die 3D-Modelle enthalten. Weiterhin ist ein Vergleich mit anderen Verfahren denkbar.

Wünschenswert sind Kenntnisse in C++ und QT, ggf. kann das Programm aber auch in einer anderen Sprache implementiert werden.

Interessentenkreis:

• Studenten der Informatik mit Interesse an Werkstofftechnik
• Studenten des Maschinenbaus mit Programmiererfahrung

Wachsende Anforderungen im Bereich des Automobilbaus an den Werkstoff Stahl im Hinblick auf geringe Kosten, hohe Ressourceneffizienz und Sicherheits-anforderungen führen zu einem ansteigenden Einsatz von hochfesten sowie höher- und höchstfesten Stählen im Karosseriebau. Bei den meisten Stählen dieser Grenzklassen werden die mechanischen Eigenschaften durch eine gezielte Mischung unterschiedlich harter Gefügebestandteile (Phasen) wie Ferrit, Bainit, Austenit und Martensit gesteuert. Für den Festigkeitsbereich von 350 – 1000 MPa gewinnen besonders Dualphasenstähle (DP-Stähle) an Bedeutung.

Das makroskopische Fließverhalten von DP-Stählen hängt im Wesentlichen von den Eigenschaften einzelner Phasen (Ferrit und Martensit) sowie der Morphologie des Martensits ab und wird seit einiger Zeit im Rahmen der numerischen Mikromechanik beschrieben. Dabei wird das makroskopische Fließverhalten mit Hilfe eines repräsentativen Volumenelements (RVE) modelliert, das einen statistisch repräsentativen Ausschnitt der Mikrostruktur des Werkstoffs im dreidimensionalen Raum darstellt.

Das Ziel der Arbeit ist, eine Methode zu entwickeln, um mit Hilfe möglichst weniger Schliffbilder eines realen DP-Stahls durch schnelle grafische Verarbeitung ein RVE als dreidimensionales Voxelmodell zu erzeugen. Das Voxelmodell sollte die statistische Verteilung und Struktur der Schnittbilder durch prozedurale Synthese nachbilden. Die im Rahmen dieser Arbeit zu entwickelnde Software soll als Plugin für die YaDiV Software in Java realisiert werden.

Quellen:

[1] A. Baddely and E.B. Vedel Jensen: Stereology for Statisticians
[2] K.J. Kurzydlowski and B. Ralph: The quantitative description of the microstructure of materials